ロードバイクタイヤの流行は23cタイヤから25cタイヤに移行しました。
すでに23cタイヤはオワコン化しつつあります。
ですが、私は23cタイヤが好きなので、これからも23cを使っていきます。
25cタイヤが流行ったきっかけになったのが「23cよりも接地面積が小さく転がり抵抗が少ない。」
または「23cタイヤよりタイヤの変形量が小さいので転がり抵抗が少ない」というものです。
整った設備で、正確に測ればそうなるのかもしれませんが、どうしても私には納得ができません。
なので、拓本をとってみました。
結果、23cの方が接地面積が小さい結果となりました。
これからやることは、実験室での精密なものではありません。
実際の実験データとの相違はあると思います。
25cの方が接地面積が広いという結果になっていますが、25cの性能を否定するものではないことをご理解ください。
【タイヤの基礎】23cは縦に長く、25cタイヤは横に広いという接地面
23cとか、25cというのはタイヤ幅です。
23cは23㎜で25cは25㎜がおおむねのサイズとなります。
実測値は23cは24㎜くらいで25cは27㎜くらいになります。
23cが25cタイヤより太くなるということはありません。
23cは25cより細いタイヤです。
700cというのはホイールの直径の企画なので、23㎜の700cと25㎜の700cのホイール直径は同じですが、タイヤの太さが25cの方が太いので外径は25cの方が大きくなります。
ここから本題。
23cは25cより細いので接地面は25cよりも小さくなります。
これはすぐに想像できますよね。
では縦(進行方向)の長さが25cの方が短くなるというのがすぐに理解できますか?
私はこの点が不思議で仕方なかったわけです。
25cの方が外径が大きいわけですが、その程度で縦の接地面積が変わるの?と思っていました。
長さと幅の違いがあったとしても総面積は?
細くて長い接地面と太くて短い接地面。
長さの違いと幅の違いがあったとしても、総面積が同じということも考えられます。
接地面が多ければ転がり抵抗は大きくなるので、縦だろうと横だろうと接地面は少ないほうがいいに決まっているんじゃないのかな?
「縦に長いと転がり方向での接触面積が大きい」としても、横に広くても転がってるんだから同じじゃないのかな?
ってことを常々思ってたから測ってみました。
わからないならやってみよう 接地面を拓本で調べてみた
23cと25cタイヤの接地面を拓本という形でとってみました。
基本的な仕様は以下の通りです。
23cは通常のリムに装着し、7barの空気圧としています
25cは23cで使うナローリムに装着し、6barと7barの2通りの空気圧としました。
23cのリヤ用が手元になかったので、前輪での測定です。
重量がある程度乗っていないとタイヤは変形しないので、ハンドルに全体重を乗せています。
体重がのっているので、前輪としては走行時よりもタイヤの変形量は大きいはずです。
後輪のイメージに近いかもしれませんが、できる限り同じ条件でやったつもりです。
拓本をとった結果、確かに25cの方が縦に短い接地面になった
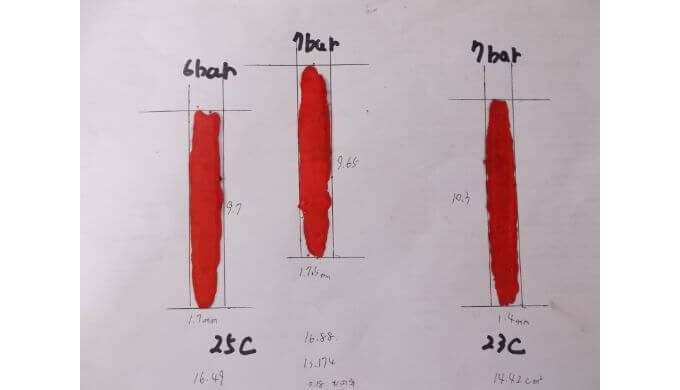
画像の左から25cの6bar、次に25cの7bar、右側のものが23cの7barです。
それぞれ縦に9.7㎝(25c 6bar)、9.65㎝(25c 7bar)、10.3cm(23c 7bar)となりました。
あきらかに25cの方が縦に短いですね。
このことから接地面積が25cの方が小さくて路面抵抗も小さい結果になりました。
とはなりません(笑)
縦に関しては25cが勝利 では横は?
当然ですが25cは横に広いです。
1.7㎝(25c 6bar)、1.65cm(25c 7bar)、1.4cm(23c 7bar)でした。
楕円の面積を計算するのが面倒くさいので、いったん長方形として計算してみました。
それぞれ16.49㎠(25c 6bar)、15.92㎠(25c 7bar)、14.42㎠(23c 7bar)ということで、最も接地面積が小さいのは23cです。
このままでも「まぁ23cの方が接地面積は小さいよね」となりますが、「タイヤの接地面は楕円だ!」という声が聞こえてきそうなので楕円で計算してみました。
やっぱり23cの方が接地面積は小さい
楕円での数値は以下のようになります。
12.9512(25c 6bar)、12.4168(25c 7bar)、11.3254(23c 7bar)
23cのほうが接地面積は小さくなりますね。
楕円率です
0.17(25c 6bar)、0.17(25c 7bar)、0.13(23c 7bar)
楕円率がどう影響するかわかりませんが参考までに。
走行中のタイヤの変形は25cの方が23cよりすくないのか?
走行中のタイヤの変形などは個人で測定することはできないのであくまでも想像ですが、高圧であれば低圧のものより変形量は小さいと考えられます。
6barの25cよりも7barの23cの方が変形量は少ないはずです。
同じ空気圧でタイヤの太さが違う場合は、タイヤの体積が大きいものの方が剛性は低いはずなので25cの方が変形量は大きいと考えます。
乗り心地とグリップでは25cのほうが圧倒的に高性能

25cはエアーボリュームがあるので乗り心地に関しては23cよりも圧倒的にいいです。
乗るとすぐにわかるほどの乗り心地なので、ロングライドメインであるなら25cの選択の方をお勧めします。
タイヤのグリップに関しても、接地面が広ければ路面との摩擦も大きくなるので25cの方が優れています。
このことから、ディスクブレーキ車には25c以上のタイヤが望ましいと思います。
タイヤのグリップ以上の制動力は発揮しないので『制動力を上げる=タイヤのグリップを上げる』ということになります。
リムブレーキでも、制動力を上げたければ25c以上のタイヤを使うべきです。
タイヤのグリップ力を超えた制動力はディスクブレーキとリムブレーキの差は全くありません。
制動力の限界 = タイヤのグリップ力の限界 です。
まとめ
25cの接地面における私なりの疑問の答えを拓本という形で出してみました。
結果、23cの方が接地面も小さく、高圧であることから変形量も小さいという結論です。
接地面が小さいということは、転がり抵抗も小さいということになるので23cの方が25cよりも軽く走れるということになるはずです。
ちなみに、今回試したタイヤは新品ではありません。
25cも23cも使用しているタイヤなので摩耗はしています。
新品だとまた違う結果になるのかもしれませんが、新品のまま走り続けることはできません。
中古の摩耗したタイヤでも、参考にはなるのではないでしょうか?
私は23cより太いタイヤをロードで使うつもりはありません。
どうしても私の中のイメージで25cより劣っているとは思えないからです。
メーカーは新しい流れを作るというビジネススタイルがあります。
しかし、ユーザーにとってはメーカーの目指すものが必要なものではない場合もあります。
私にとっては23c以上のタイヤはロードでは必要のないサイズです。
実測した数値が正しいとは思っていませんが、タイヤの選択の参考にしていただければと思います。




コメント